научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
# 05, май 2013
DOI: 10.7463/0513.0551477
УДК 621.396
Россия, МГТУ им. Н.Э. Баумана
Введение
Внедрение спутниковых радионавигационных и радиосвязных систем породил повышенный интерес к системам синхронизации, к их точности и помехозащищенности.
Все эти системы работают в условиях воздействия помех [1-3].
Дальнейшее усовершенствование систем синхронизации за счет улучшения конструктивных и технологических решений имеет предел, вызываемый воздействием флуктуаций и помех естественного и искусственного происхождения.
Помехоустойчивости систем синхронизации посвящен ряд работ [4, 5, 7 и др.].
В данной статье путем анализа фазовых портретов ФАП получены уравнения захвата за сигнал и за гармоническую помеху.
1. Влияние гармонической помехи на систему ФАП второго порядка
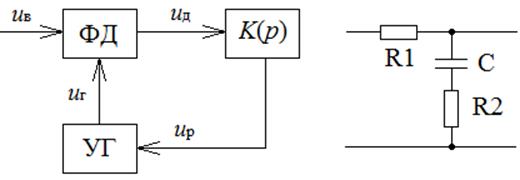
Функциональная схема ФАП второго порядка приведена на рис. 1,а, где uв – смесь сигнала и гармонической помехи, uд – напряжение на выходе фазового детектора (ФД), uр – напряжение на выходе фильтра, uг – сигнал управляемого генератора (УГ). Данная схема отличается от схемы первого порядка наличием пропорционально-интегрирующего фильтра (ПИФ) на выходе фазового детектора приведенного на рис. 1,б.
На вход системы воздействует аддитивная смесь сигнала и гармонической помехи. Дифференциальное уравнение ФАП в символической форме имеет вид [6]
![]() (1)
(1)
где ![]() – отношение помеха/сигнал; Ас, Ап – соответственно амплитуды колебаний сигнала и помехи; t1,c – время; Ω – полоса синхронизации ФАП;
– отношение помеха/сигнал; Ас, Ап – соответственно амплитуды колебаний сигнала и помехи; t1,c – время; Ω – полоса синхронизации ФАП; ![]() – расстройка частоты сигнала ωс и частоты УГ ω0;
– расстройка частоты сигнала ωс и частоты УГ ω0; ![]() – разность частот помехи и сигнала
– разность частот помехи и сигнала ![]() – оператор дифференцирования,
– оператор дифференцирования, ![]() – передаточная функция ПИФ.
– передаточная функция ПИФ.
Дифференциальное уравнение (1) может быть записано в форме
![]() (2)
(2)
где ![]() φп – фаза колебания помехи детектируемая ФД в момент времени t1.
φп – фаза колебания помехи детектируемая ФД в момент времени t1.
Введем обозначения
![]() (3)
(3)
а) | б) |
Рис. 1. Функциональная схема ФАП второго порядка
Преобразуем передаточную функцию ПИФ к виду
![]() (4)
(4)
где ![]()
![]()
![]() - постоянная времени ФНЧ;
- постоянная времени ФНЧ; ![]()
![]() соответствует вырожденному ПИФ.
соответствует вырожденному ПИФ.
Тогда второе слагаемое в (1) можно записать в виде
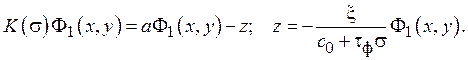 (5)
(5)
При условии (3) уравнению (2) можно сопоставить систему из трех дифференциальных уравнений первого порядка
![]() (6)
(6)
где ![]() f – некоторая вектор-функция переменных x, y, z.
f – некоторая вектор-функция переменных x, y, z.
Третье уравнение системы сразу получаем из (5)
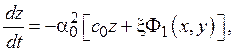
где ![]()
По уравнению (3) находим
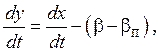 (7)
(7)
где ![]()
![]()
С учетом (3) по уравнению (2) получаем
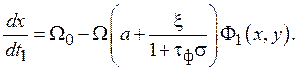
Отсюда
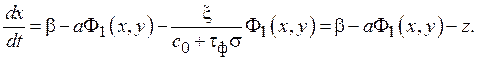
Обозначим [7]
![]()
тогда из искомой системы дифференциальных уравнений получим первое дифференциальное уравнение

и с учетом (7) второе дифференциальное уравнение
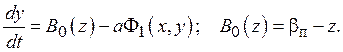
Итак, система дифференциальных уравнений (6) окончательно принимает вид [7]
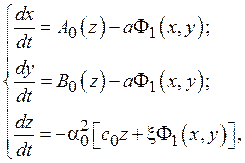 (8)
(8)
Рассмотрим частный случай ФАП первого порядка. Тогда при ![]() по третьему уравнению системы получим
по третьему уравнению системы получим
![]()
В результате по системе из трех дифференциальных уравнений (8) находим систему из двух дифференциальных уравнений
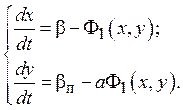
Введем параметр ![]() и обозначим
и обозначим ![]() Тогда по (8) получим систему дифференциальных уравнений
Тогда по (8) получим систему дифференциальных уравнений
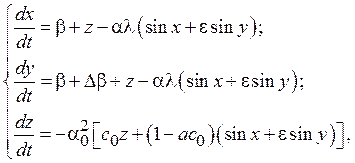 (9)
(9)
где ![]()
Процедуру усреднения [8] можно применять в случае, если ![]() тогда
тогда ![]() а
а ![]() и сохраняет постоянное значение. В этом случае переменные xи y изменяются быстро, а переменная z– медленно.
и сохраняет постоянное значение. В этом случае переменные xи y изменяются быстро, а переменная z– медленно.
Будем искать решение системы дифференциальных уравнений (9) в виде
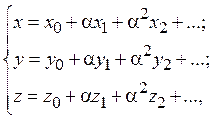
т.е. каждую из переменных состояния представляем функциональным рядом с коэффициентами, являющиеся степенями малого параметра α. Будем учитывать нулевое, первое и второе слагаемые функционального ряда и пренебрегать слагаемыми, содержащие α3 и более высокие степени α. Функции в правой части соотношений для x, y, zзависят от времени явно: ![]()
![]()
![]() и неявно:
и неявно: ![]()
![]()
![]() и т.д.
и т.д.
Пусть также выполняются равенства
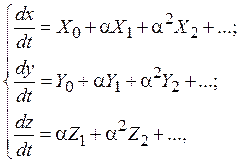
т.е. правые части дифференциальных уравнений, описывающих ФАП, так же могут быть представлены в виде функциональных рядов с коэффициентами, которые есть не что иное, как степени малого параметра α. Будем учитывать слагаемые функциональных рядов с нулевого по второе включительно и пренебрегать остальными (нулевое слагаемое функционального ряда для ![]() очевидно, равно нулю). Заметим также, что по предположению функции
очевидно, равно нулю). Заметим также, что по предположению функции ![]() … зависят от времени только неявно:
… зависят от времени только неявно: ![]()
![]()
![]() ,…
,…
Получим соотношения, связывающие друг с другом переменные x0, y0, z0, x1, y1, z1, x2, y2, z2 и X0, Y0, X1, Y1, Z1, X2, Y2, Z2. Для этого продифференцируем выражения для x, y, zпо времени t:
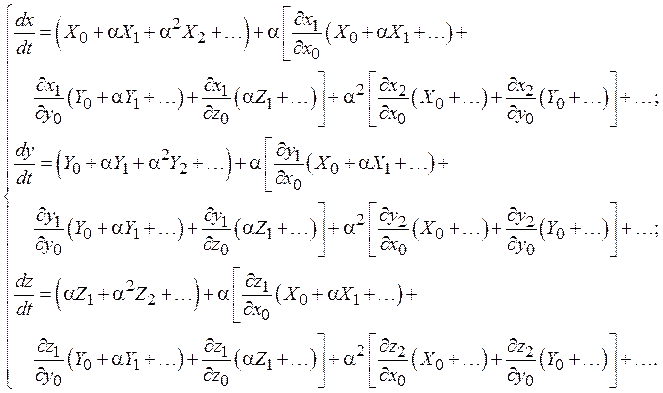
С другой стороны, справедливы дифференциальные уравнения, задающие модель ФАП. Подставим в их правые части соотношений для x, y, zи разложим функции sinxи sinyв ряды Тейлора в окрестности точек x0 и y0:
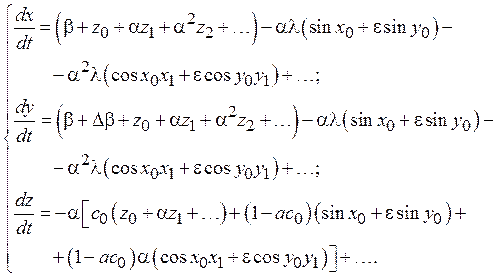
Приравнивая в правых частях выражений для ![]()
![]() и
и ![]() слагаемые, содержащие в качестве сомножителей одинаковые степени параметра α, получаем
слагаемые, содержащие в качестве сомножителей одинаковые степени параметра α, получаем
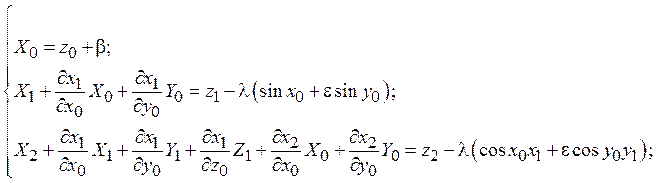
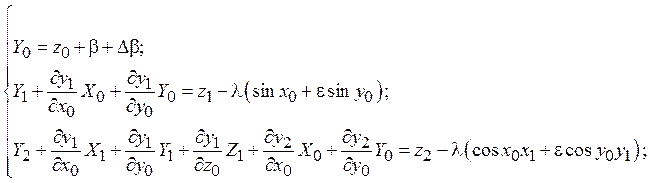
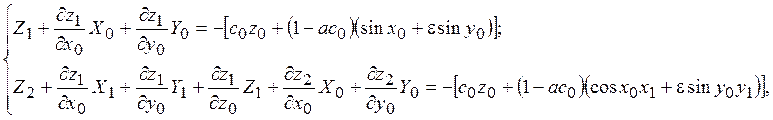
Теперь необходимо учесть, что если применяется процедура усреднения, то функции x1, y1, z1, x2, y2, z2 периодические (с периодом 2π) по переменным x0 и y0, либо зависят от одной из этих переменных. Следовательно,
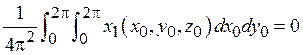
и т.п., так как среднее за период значение этих функций учитывается слагаемыми x0, y0 и равно нулю.
Проинтегрируем полученные выше уравнения связи функций x0, y0, z0, x1, y1, z1, x2, y2, z2 и X0, Y0, Z1, X1, Y1, Z1, X2, Y2, Z2 в пределах ![]() по x0, y0, разделив полученные равенства на
по x0, y0, разделив полученные равенства на ![]() . Тогда ясно, что
. Тогда ясно, что
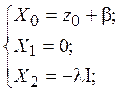
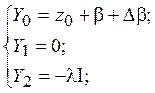
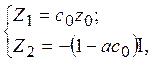
где 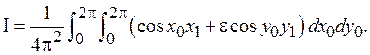
С учетом полученных равенств уравнения связи упрощаются:
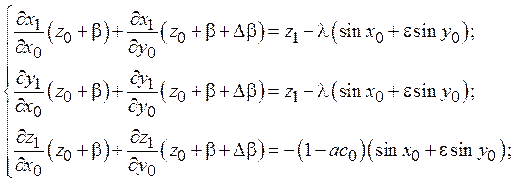
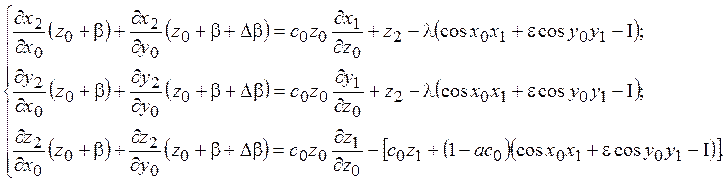
Исключая из трех первых уравнений функцию z1, убеждаемся, что
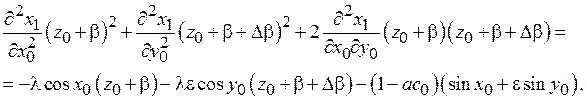
Аналогичное уравнение справедливо для функции y1.
Чтобы ![]() необходимо, чтобы функция x1=x1(x0, y0, z0) не зависела от y0 или по крайней мере содержала слагаемое, не зависящее от y0:
необходимо, чтобы функция x1=x1(x0, y0, z0) не зависела от y0 или по крайней мере содержала слагаемое, не зависящее от y0: ![]() Тогда умножая последнее дифференциальное уравнение в частных производных на cosx0, интегрируя в пределах
Тогда умножая последнее дифференциальное уравнение в частных производных на cosx0, интегрируя в пределах ![]() по x0 и y0, и, наконец, разделив результат на 4π2, получаем
по x0 и y0, и, наконец, разделив результат на 4π2, получаем
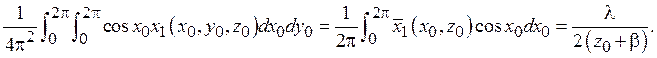
Аналогично, чтобы ![]() необходимо, чтобы функция y1=y1(x0, y0, z0) не зависела от x0 или по крайней мере содержала слагаемое, не зависящее от x0:
необходимо, чтобы функция y1=y1(x0, y0, z0) не зависела от x0 или по крайней мере содержала слагаемое, не зависящее от x0: ![]() Тогда умножая последнее дифференциальное уравнение в частных производных на cosy0, интегрируя в пределах
Тогда умножая последнее дифференциальное уравнение в частных производных на cosy0, интегрируя в пределах ![]() по x0 и y0, и, наконец, разделив результат на 4π2, получаем
по x0 и y0, и, наконец, разделив результат на 4π2, получаем
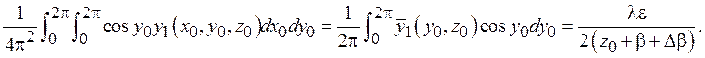
Отсюда имеем
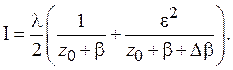
Таким образом, найдены явные выражения через z0 для функций X0, Y0, Z1, доказано, что X1=0, Y1=0. Теперь с учетом явного выражения интеграла Iчерез z0 получаем соотношения для функций X2, Y2, Z2:
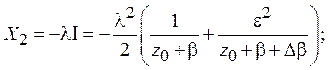
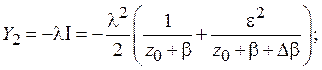
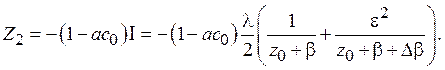
Следовательно, можно записать систему дифференциальных уравнений для функций x0, y0, z0, правые части которой согласно сделанным предположениям зависят только от функций X0, Y0, X1, Y1, Z1 и X2, Y2, Z2:
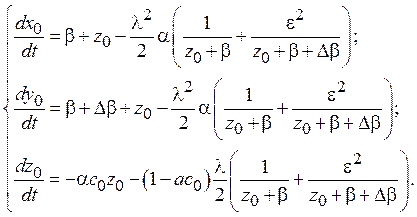 (10)
(10)
Система дифференциальных уравнений (10) является усредненной системой дифференциальных уравнений, решение которой аппроксимирует истинное решение системы дифференциальных уравнений, задающей модель ФАП, с точностью до слагаемых порядка α. Нетрудно убедиться, что усредненная система дифференциальных уравнений проще исходной. В дальнейшем рассматривается только эта система дифференциальных уравнений, по свойствам которой будем судить о свойствах ФАП второго порядка при наличии гармонической помехи.
При c0=1 (невырожденный ПИФ) нельзя провести аналитическое интегрирование последнего уравнения усредненной системы (10). Однако при больших значениях постоянной времени ПИФ можно пренебречь величиной c0 и положить c0=0, что соответствует вырожденному ПИФ. Рассмотрим последнее дифференциальное уравнение системы (10) при этом условии:
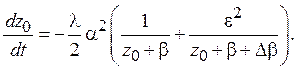
Разделяя переменные и производя интегрирование, находим
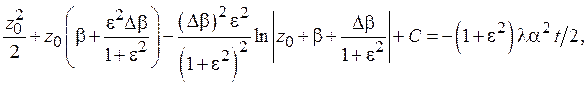
где C – произвольная постоянная. Если положить
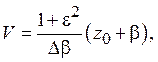
то получим
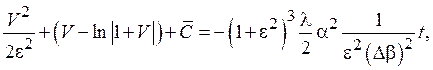
где ![]() – новая произвольная постоянная, связанная с Cсоотношением
– новая произвольная постоянная, связанная с Cсоотношением

Введем также новое время

Тогда окончательно получаем
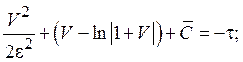
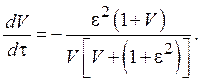
Зависимости ![]() могут быть заданы только неявно. Функция
могут быть заданы только неявно. Функция ![]() имеет два минимума в точках
имеет два минимума в точках ![]() и
и ![]() а также вертикальную асимптоту в точке
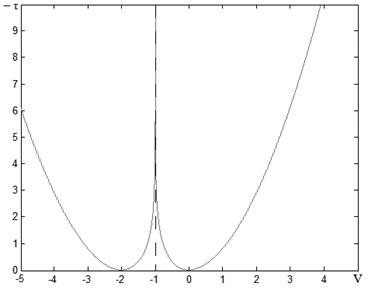
а также вертикальную асимптоту в точке ![]() На рис. 2 приведены графики функций
На рис. 2 приведены графики функций ![]() при
при ![]() и различных ε: ε=0.6 (рис. 2, а), ε=1 (рис. 2, б) и ε=1.4 (рис. 2, в).
и различных ε: ε=0.6 (рис. 2, а), ε=1 (рис. 2, б) и ε=1.4 (рис. 2, в).
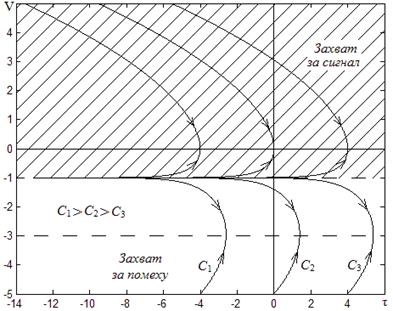
Результаты представлены на рис. 3, а-в. Для различных значений ![]() (4; 0; -4) заметим также, что из выражения для производной
(4; 0; -4) заметим также, что из выражения для производной ![]() следует, что функция
следует, что функция ![]() возрастает при
возрастает при ![]() ,
, ![]() и убывает при
и убывает при ![]() ,
, ![]() Направление изменения функции
Направление изменения функции ![]() с ростом τ показано на рис. 3 стрелками.
с ростом τ показано на рис. 3 стрелками.
В результате можно сделать вывод, что, задав начальный момент времени ![]() и начальное значение переменной
и начальное значение переменной ![]() равное
равное ![]() можно однозначно определить решение дифференциального уравнения для переменной
можно однозначно определить решение дифференциального уравнения для переменной ![]() соответствующее данным начальным условиям. Процесс поиска такого решения показан на рис. 3 штрихпунктирными линиями. Если
соответствующее данным начальным условиям. Процесс поиска такого решения показан на рис. 3 штрихпунктирными линиями. Если ![]() то процесс изменения переменной
то процесс изменения переменной ![]() заканчивается в точке
заканчивается в точке ![]() или же
или же ![]() при этом, как следует из второго дифференциального уравнения усредненной системы, установившееся значение переменной
при этом, как следует из второго дифференциального уравнения усредненной системы, установившееся значение переменной ![]() компенсирует первоначальную частотную расстройку между помехой и свободными колебаниями генератора, входящего в состав ФАП, т.е. происходит захват за помеху. Если
компенсирует первоначальную частотную расстройку между помехой и свободными колебаниями генератора, входящего в состав ФАП, т.е. происходит захват за помеху. Если ![]() то процесс изменения переменной
то процесс изменения переменной ![]() заканчивается в точке
заканчивается в точке ![]() (или
(или ![]() ). При этом, как следует из первого дифференциального уравнения усредненной системы, установившееся значение переменной
). При этом, как следует из первого дифференциального уравнения усредненной системы, установившееся значение переменной ![]() компенсирует первоначальную частотную расстройку между сигналом и свободными колебаниями генератора, т.е. происходит захват за сигнал. Задав начальное значение переменной
компенсирует первоначальную частотную расстройку между сигналом и свободными колебаниями генератора, т.е. происходит захват за сигнал. Задав начальное значение переменной ![]() равное
равное ![]() из неравенства
из неравенства
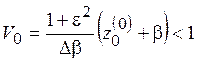

а) | б) |

в)
Рис. 2. Графики зависимости функции ![]() от
от ![]() при различных значениях ε
при различных значениях ε
можно определить границы области захвата за помеху на плоскости параметров ![]() :
:
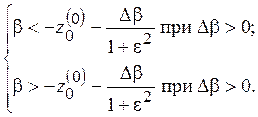
Аналогично определяются границы области захвата за сигнал:
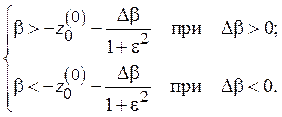
а) | б) |
в)
Рис. 3. Графики зависимости функции ![]() от
от ![]() при различных значениях ε и С
при различных значениях ε и С
На рис. 4 приведена бифуркационная диаграмма ФАП второго порядка при наличии гармонической помехи на плоскости параметров ![]() , если начальное значение переменной
, если начальное значение переменной ![]() равно
равно ![]()
Из полученной диаграммы следует, что режим работы системы определяется не только частотными расстройками сигнала и помехи (параметры β и Δβ), но и начальным значением переменной z0. Это говорит о том, что на режим захвата оказывает влияние предыстория работы системы.
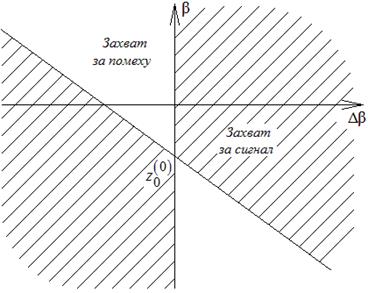
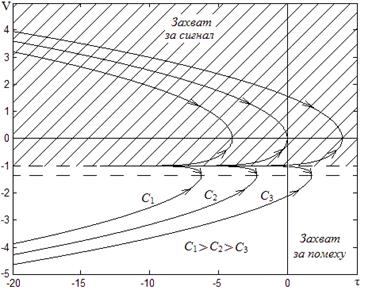
Рис. 4. Бифуркационная диаграмма ФАП второго порядка
Из диаграммы также следует, если система находиться в режиме захвата за сигнал  , то перейти в режим захвата за помеху она не может ни при каких ε и Δβ. Однако, с практической точки зрения помеха должна оказывать влияние на процесс синхронизации. Для исследования этого влияния обратимся к численному решению системы дифференциальных уравнений (9).
, то перейти в режим захвата за помеху она не может ни при каких ε и Δβ. Однако, с практической точки зрения помеха должна оказывать влияние на процесс синхронизации. Для исследования этого влияния обратимся к численному решению системы дифференциальных уравнений (9).
Проведенное методом Рунге-Кутты четвертого порядка численное решение системы (9) показало, что при определенной интенсивности помехи происходит ее захват. Поиск критических значений Δβ проводился при условии, что система осуществляет слежение за сигналом  и при отсутствии сигнальной частотной расстройки (β=0). На рис. 5 квадратными метками показаны критические значения Δβ, при которых происходит смена режима захвата.
и при отсутствии сигнальной частотной расстройки (β=0). На рис. 5 квадратными метками показаны критические значения Δβ, при которых происходит смена режима захвата.
При малых значениях Δβ (≈0,1) и близких амплитудах сигнала и помехи (ε≈1) в системе возникают асинхронные движения (заштрихованная область на рис. 5). ФАП не может осуществить захвата ни помехи, ни сигнала, а осуществляет синхронизацию на некоторой промежуточной частоте.
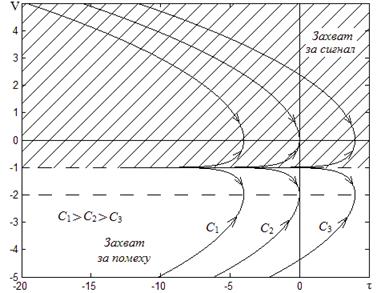
С учетом полученных результатов бифуркационная диаграмма при ε=2 принимает вид рис. 6. Здесь в отличие от рис. 4 имеется участок, на котором происходит захват помехи (при ε>1) при любых значениях β и ![]() .
.

Рис. 5. График зависимости ε от β
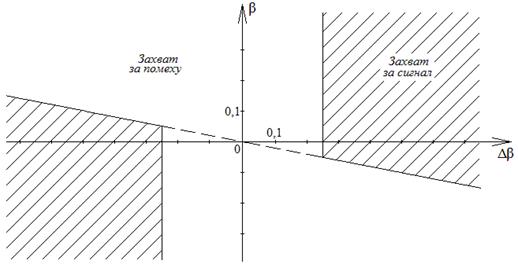
Рис. 6. Бифуркационная диаграмма ФАП
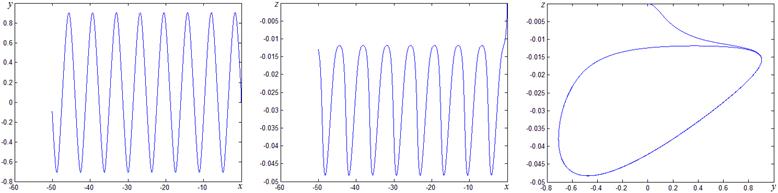
Характер движений, возникающих в системе при различной интенсивности помехи, иллюстрируют рис. 7-8, где изображены проекции фазовой траектории на плоскости (x,y), (x,z), (y,z). Рис. 7 соответствует режиму захвата за сигнал (Δβ=0,1; ε=0,6; a=0.8; α=0.16), рис. 8 – режиму захвата за помеху (Δβ=0,1; ε=1,4 a=0.8; α=0.16).
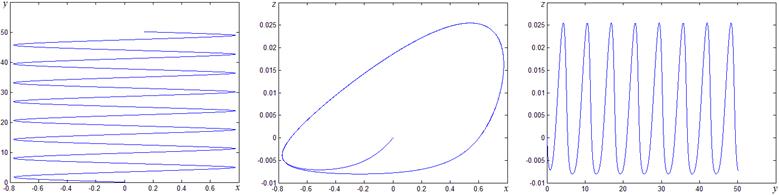
а) | б) | в) |
Рис. 7. Проекция фазовой траектории на плоскости в режиме захвата сигнала
а) | б) | в) |
Рис. 8. Проекция фазовой траектории на плоскости в режиме захвата помехи
Используемый численный метод решения системы дифференциальных уравнений позволяет получить зависимости, аналогичные рис. 5, в случае невырожденного ПИФ в кольце ФАП (c0=1). Параметры системы аналогичны случаю вырожденного ПИФ (a=0,05; α=0,01). Сравнивая рис. 9 с рис. 5, можно заметить, что характер зависимости практически не изменился, отличие состоит лишь в размерах области неустойчивой синхронизации при малых Δβ=0,1 и ε≈1. Это подтверждает, что при больших τф можно без больших потерь рассматривать случай вырожденного ПИФ в кольце ФАП.
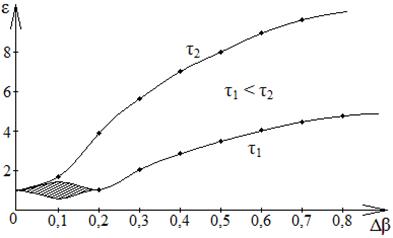
Рис. 9. График зависимости ε от β
Рассмотрим влияние полосы пропускания ПИФ на процессы захвата сигнала или помехи. На рис. 9 треугольными метками показаны результаты численных расчетов при a=0,01; α=0,005, что соответствует увеличению постоянной времени ПИФ в пять раз по сравнению с предыдущем случаем. Из полученных зависимостей следует, что увеличение постоянной времени фильтра (уменьшение полосы пропускания) повышает помехоустойчивость системы. Однако, при малых Δβ достаточно незначительного превышения амплитуды помехи над амплитудой сигнала, чтобы произошел захват за помеху.
В заключение рассмотрим определение времени переходного процесса, т.е. промежутка времени, за которой ФАП компенсирует первоначальную частотную расстройку и произойдет захват за сигнал либо за помеху.
Пусть ![]() или, что то же самое,
или, что то же самое, ![]() Тогда конец процесса регулирования частоты – это достижение точки V=0 и захвата за сигнал. Зависимость
Тогда конец процесса регулирования частоты – это достижение точки V=0 и захвата за сигнал. Зависимость ![]() соответствующая такому процессу, соединяет точки (τ0,V0) и (τk,Vk). При этом τk – τ0 =Δτ – длительность переходного процесса;
соответствующая такому процессу, соединяет точки (τ0,V0) и (τk,Vk). При этом τk – τ0 =Δτ – длительность переходного процесса; ![]() – соответственно начальные и конечные значения переменных
– соответственно начальные и конечные значения переменных ![]() Так как обе точки лежат на одной и той же кривой, то
Так как обе точки лежат на одной и той же кривой, то

Вычитая из первого равенства второе, имеем длительность переходного процесса при захвате за сигнал
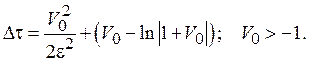
Аналогично из равенств

вытекающих из того факта, что при ![]() и захвате за помеху зависимость
и захвате за помеху зависимость ![]() соответствующая процессу регулирования частоты, соединяет точки (τ0,V0) и (τk,Vk), причем
соответствующая процессу регулирования частоты, соединяет точки (τ0,V0) и (τk,Vk), причем ![]() может быть получена длительность переходного процесса при захвате за помеху:
может быть получена длительность переходного процесса при захвате за помеху:

Приложение
Найдем критические значения первой гармоники x1=x1k и отношения помеха/сигнал ε=εk, которые определяют условия срыва синхронизации:
![]() (П.1)
(П.1)
При учете второго условия по уравнению

находим ![]() . Отсюда следует
. Отсюда следует
![]()
При учете первого равенства в (П.1), находим
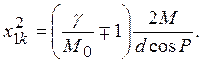
Подставляя это значение ![]() в (П.1) окончательно получим
в (П.1) окончательно получим
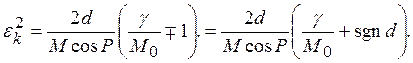
Зависимость ![]() при a=0.8 и
при a=0.8 и ![]() изображена на рис. П.1, где прямая 1 получена при ФАП 1-го порядка и β=0; прямая 2 при невырожденном и вырожденном фильтре и β=0; 3 – ФАП 1-го порядка β=0.8; 4 - невырожденный и вырожденный фильтр и β=0.8;
изображена на рис. П.1, где прямая 1 получена при ФАП 1-го порядка и β=0; прямая 2 при невырожденном и вырожденном фильтре и β=0; 3 – ФАП 1-го порядка β=0.8; 4 - невырожденный и вырожденный фильтр и β=0.8;
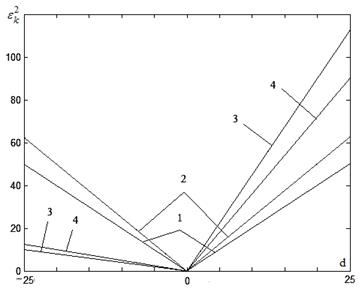
Рисунок П.1
По рис. П.1 замечаем, что при β>0 и d>0 помехоустойчивость ФАП выше, чем β>0, а d<0.
Можно показать, что условиями захвата за сигнал при действии гармонической помехи является [5] условие
![]()
или условие
![]()
С другой стороны, по [9] находим
![]()
или
![]()
Причем во втором случае границы захвата по сигналу совпадают с [4] несмотря на то, что получены [4,5] и [9] на основе разных критериев.
Достаточным условием захвата за помеху является условие [5]

или
![]()
При этом левая граница в данном случае совпадает с [4].
Заключение
Таким образом, в результате проведенного анализа были получены условия захвата за сигнал и за помеху, зависящие от отношения помеха/сигнал (ОПС), и получены проекции фазовой траектории на плоскости в режиме захвата сигнала и захвата помехи, а также графики зависимостей ОПС от начальной расстройки по частоте. Кроме того, представлены данные сравнения критических значений параметров, полученных двумя различными методами.
Список литературы
1. Шахтарин Б.И. Анализ систем синхронизации при наличии помех. М.: ИПРЖР, 1996. 252 с.
2. Meyr H., Ascheid G. Synchronization in digital communications frequency – locked loops, and amplitude control. N.Y.: Wiley, 1990. 510 p.
3. Stephens D.R. Phase – locked loops -for Wireless communications. Digital, analog and implementations. 2nd ed. N.Y.: Kluwer, 2002. 421 p.
4. Шахтарин Б.И. Анализ систем синхронизации методом усреднения. М.: Радио и связь, 1999. 495 с.
5. Nakagawa M. Effects of interfering signals in phase-locked loops // Frequentz. 1978. Vol. 32, no. 5. P. 146-153.
6. Шахтарин Б.И. Квазигармонический метод и его применение к анализу нелинейных фазовых систем. М.: Энергоатомиздат, 1987. 192 с.
7. Быховский М.А. Влияние помехи на процессы захвата в системе фазовой автоподстройки частоты // Радиотехника и электроника. 1987. № 10. С. 2131-2141.
8. Richman D. Color-carrier reference phase synchronization accuracy in NTSC color television // Proc. IRE. 1954. Vol. 42, no. 1. P. 106-133.
9. Karsi M.F., Lindsey W.C. Effects of CW interference on phase-locked performance // IEEE Trans. 2000. Vol. COM-48, no. 5. P. 886-896.
Публикации с ключевыми словами: помехоустойчивость, фазовая автоподстройка, гармоническая помеха, отношение помеха/сигнал
Публикации со словами: помехоустойчивость, фазовая автоподстройка, гармоническая помеха, отношение помеха/сигнал
Смотри также:
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



