научное издание МГТУ им. Н.Э. Баумана
НАУКА и ОБРАЗОВАНИЕ
Издатель ФГБОУ ВПО "МГТУ им. Н.Э. Баумана". Эл № ФС 77 - 48211. ISSN 1994-0408
#1 ноябрь 2003
Тухватуллина Светлана Айратовна
средняя школа ╧ 1941, 11 класс
Научный руководитель:
Хорохоров Алексей Михайлович,
кандидат технических наук,
доцент кафедры «Лазерные и оптико-электронные системы»
МГТУ им. Н.Э.Баумана
ВВЕДЕНИЕ
Гауссов пучок – это важное понятие, оно с разных сторон объясняет световой пучок, создаваемый лазером. В отличие от лучей, относящихся к геометрической оптике, в которой волновой природой света пренебрегают, гауссов пучок является волновым явлением, в котором дифракция играет ключевую роль в его распространении. Законы формирования лазерного пучков впервые были описаны на основе теории дифракции на языке волновой оптики. В связи с этим существует мнение, что геометрическая оптика неприменима к описанию особенностей формирования и преобразования лазерных пучков. Вместе с тем, идея о применимости геометрической оптики к указанным задачам появилась давно, более 30 лет назад.
В работе показано, что распространение гауссового пучка, включая его взаимодействие с оптическими компонентами, такими как линзы и зеркала, могут быть описаны простым расширением понятий геометрической оптики. Фактически, мы продемонстрируем, что, возможно, описать распространение такого луча, используя чертежи, основанные только на Евклидовой геометрии. Все, что необходимо для решения проблемы, это линейка и циркуль.
Знания только школьной геометрии позволяют решить много интересных проблем, такие, например как изменение формы гауссового пучка и его параметров.
Геометрические методы отличаются наглядностью результатов и простотой применения. В значительной степени упрощается и задача синтеза оптических систем преобразования лазерного излучения.
Предлагаемая работа посвящена применению геометрических методов описания преобразования гауссовых лазерных пучков и анализу сопоставимости выводов геометрического метода и волнового расчета. В работе показано, что теоремы геометрии могут быть использованы для обеспечения различных подходов к решаемой задаче. Если требуются точные численные ответы, то они всегда могут быть получены с применением геометрии и тригонометрии к представленным схемам.
ЭРМИТО-ГАУССОВЫЙ ПУЧОК
Как известно [1,4], гауссов пучок, образуемый в лазерах с устойчивым резонатором, характеризуется следующими параметрами:
· радиусом r пучка по уровню ![]() для интенсивности:
для интенсивности:
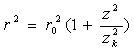 (1)
(1)
Здесь r0 – минимальный радиус пучка (по уровню ![]() ) в перетяжке, определяемый выражением
) в перетяжке, определяемый выражением
![]() , (2)
, (2)
где zk называется параметром конфокальности гауссового пучка, ![]() – длина волны лазерного излучения;
– длина волны лазерного излучения;
· расходимостью излучения:
![]() , (3)
, (3)
· радиусом волнового фронта R в произвольном сечении пучка на расстоянии z от перетяжки:
![]() (4)
(4)
Выражение (4) показывает, что радиус волнового фронта принимает бесконечно большое значение в перетяжке (z = 0) и на бесконечности. Минимальное значение радиуса волнового фронта будет в сечении z = zk. Это дает основание трактовать zk как расстояние от перетяжки, на котором радиус волнового фронта принимает минимальное значение ![]() .
.
С другой стороны из соотношения (2) следует, что zk с точностью до коэффициента пропорциональности ![]() равен площади сечения кружка в перетяжке.
равен площади сечения кружка в перетяжке.
Распределение электромагнитного поля в произвольном сечении пучка описывается гауссоидой:
![]() , (5)
, (5)
а распределение интенсивности:
![]() (6)
(6)
Если эрмито-гауссовый пучок падает на линзу с фокусным расстоянием f, то, воспользовавшись известным выводом в теории дифракции Френеля о подобии распределения полей в оптически сопряженных плоскостях линзы, можно определить параметры поля в произвольной плоскости.
Порядок действия следующий:
1) Для заданного значения а/ графически или по формуле линзы находим размер – а
-1/a + 1/a/ = 1/f/
2) Определяем расстояние z от перетяжки лазерного пучка до плоскости ОП
f/ - zp = -a + z,
отсюда:
z = -zp + a + f/
3) По формуле (6) определяем распределение интенсивности в плоскости ОП
![]()
где r берем из (1).
4) Распределение интенсивности в плоскости ОП/ будет аналогичным
![]() ,
,
где
r/2 = r2 b2= r2 a/2/a2
Из условия равенства потоков излучения в кружках ОП и ОП/ получим соотношение, связывающее Io/ и Io
Io/ = Io r2/r/2 = Io(a/a/)2 = Io/b2 ,
где b – линейное увеличение в плоскостях ОП и ОП/.
Рассмотренный метод прост; он известен давно [1] и с успехом может использоваться при необходимости определения параметров гауссового пучка в каком-либо сечении за линзой. В частности, из него немедленно следует, что расходимость лазерного пучка после линзы равна
 ,
,
где ![]() – радиус гауссового пучка в передней фокальной плоскости линзы.
– радиус гауссового пучка в передней фокальной плоскости линзы.
Для дальнейшего рассмотрения отметим ряд геометрических особенностей лазерного пучка. Представим уравнение (4) в следующем виде:
(R – z)z = zk2 (7)
Отсюда следует, что центр кривизны волнового фронта в произвольной точке А и сама точка А находятся по разные стороны от начала координат (т.е. от перетяжки гауссового пучка). Точка С приближается к перетяжке лишь в случае больших z, т.е. когда т. А стремится к бесконечности.
Гораздо более интересное геометрическое построение, вытекающие из (7), связано с теоремой о перпендикуляре, опущенном из вершины прямого угла на гипотенузу. Восстановим из центра перетяжки т. О лазерного пучка перпендикуляр к оси размером zk (определяющим, кстати, радиус перетяжки ro). Получим т. В. Тогда для того, чтобы найти значение радиуса волнового фронта в произвольной точке А и положение его центра (т. С) достаточно провести отрезок АВ и восстановить к нему перпендикуляр в т. В до пересечения с осью в точке С.
Тогда, согласно указанной теореме можно записать: OB2 = OC*OA или с учетом обозначений: zk2 = z (R-z), что точно совпадает с (7). Поскольку любой прямой угол можно трактовать как вписанный в окружность угол, опирающийся на диаметр, то это значит, что радиус волнового фронта в произвольной точке А гауссова пучка равен диаметру АС окружности, проходящей через точки А и В.
Указанные построения дают возможность трактовать ординаты этой окружности как геометрическое место точек всех возможных параметров конфокальностей zk гауссовых пучков, имеющих в точке А определенный радиус R волнового фронта.
ПРЕОБРАЗОВАНИЕ ГАУССОВОГО ПУЧКА ЛИНЗОЙ
Как известно [3, 4], радиус волнового фронта при прохождении через идеальную тонкую линзу преобразуется согласно формуле линзы:
1/R1+1/R2=1/f, (8)
где R1 и R2 – радиусы волновых фронтов на входе и выходе линзы, f – фокусное расстояние линзы.
Если на линзу падает гауссов пучок, то для нахождения параметров гауссового пучка на выходе линзы при известных параметрах на входе воспользуемся введенными ранее геометрическими построениями для гауссового пучка. Из формулы (8) следует, что центры волновых фронтов С1 и С2 на входе и выходе линзы являются оптически сопряженными. Поэтому при известных значениях R1 и С1 на входе линзы построением хода луча легко найти т. С2 и, следовательно, R2=АС2.
На линзу падает гауссов пучок, перетяжка которого находится в т. О1, а параметр конфокальности zk = ОВ1. Если положение линзы (т. А) задано, то легко определить т. С1 – центр кривизны волнового фронта пучка, падающего на линзу (АС1=R1). Прежде всего найдем точку С2 оптически сопряженную с С1. Для этого воспользуемся лучом С1В1, который продлим до линзы (точка Р) и найдем ход преломленного луча РС2 с помощью вспомогательного луча АМ//С1Р. Отрезок АС2=R2, поэтому проведем окружность диаметром R2. Точка пересечения В2 этой окружности c прямой РС2 определит положение перетяжки (точки О2) и параметр конфокальности zk=О2В2 преобразованного гауссового пучка. Сделанный вывод становится еще более очевидным, если учесть, что отрезки АР, О1В1 и О2В2 пропорциональны площадям соответственно гауссового пучка на линзе и в плоскостях перетяжки на входе и выходе. Действительно, так как zk пропорционален ro2, то из (1) и (4) можно получить:
r2/ro2=R/(R-z) (9)
В тоже время, из подобия треугольников следует:
РА/zk=AC1/O2C2 =R1/(R1-z1) = r2/ro21;
PA/zk2=AC2/O2C2 =R2/(R2-z2) =r2/ro22;
Поскольку из (2)
![]() и
и ![]() ,
,
то из последних соотношений следует
![]() ,
,
т.е. отрезок РА пропорционален площади лазерного пятна на линзе, и коэффициент пропорциональности равен ![]() .
.
Таким образом, алгоритм нахождения параметров гауссового пучка, преобразованного линзой, выглядит так:
1) Из точки О1, определяющей положение перетяжки исходного пучка, восстанавливаем перпендикуляр к оси линзы и откладываем на нем отрезок О1В1= ![]()
2) Проводим линию от центра линзы (точка А) к точке В1.
3) Проводим перпендикуляр к линии АВ1 в точке В1 до пересечения с оптической осью в точке С1.
4) Продолжим отрезок В1С1 до пересечения с линзой в точке Р. Отрезок АР характеризует пятно на линзе.
5) Методами геометрической оптики находим изображение точки С1, т. е. точку С2.
6) Проводим линию РС2 и от центры линзы (точка А), восстанавливаем перпендикуляр к этой линии до пересечения в точке В2.
7) Перпендикуляр из точки В2 на оптическую ось определяет положение новой перетяжки, а отрезок О2В2=zk2 – параметр конфокальности преобразованного пучка.
Окончательным подтверждением правильности изложенных геометрических построений должно быть соответствие параметров преобразованного гауссового пучка формулам, полученных на основе дифракционной теории. Известно, что параметры преобразованного гауссового пучка определяются соотношениями:
![]() , , (10)
, , (10)
где
aг = f2/(zp2 +zk2) (11)
Для доказательства такого соответствия рассмотрим расчетную схему.Введем систему координат ХY с началом в точке А и обозначим y1(x) и y2(x) – уравнения прямых С1Р и С2Р, y/1(x) и y/2(x) – уравнения прямых АВ1 и АВ2 .
Очевидно,
y1(x) = k1x+b
y2(x) = k2x+b (12)
y1/(x) = (-1/k1)*x
y2/(x) = (-1/k1)*x,
где
k1 = tga, k2 = tga2,
b = AP,
а k1 и k2 связаны соотношением:
k2=(k1f-b)/f
Соединим фокусы линзы и точки В1 и В2 и обозначим z1=FB1 и z2 =F/B2, тогда, очевидно, что z12= zp12+zk12, следовательно, aг= f2/z12. Продолжим прямые FB1 и F/B2 и, прежде всего, покажем, что их точка пересечения N находится на линзе. Для этого найдем координаты точек пересечения В1(xo1;yo1) и В2(Xo2;xo2).
Получим:
xo1 = - bk1/(k12+1),
yo1=- b/(k12+1),
xo2= - bk2/(k22+1),
yo2=- b/(k22+1).
Найдем:
tgg1 = yo1/(f+ xo1) = (b/(k12+1))/(f- bk1/(k12+1)) = b/(f(k21+1)-bk1).
Аналогично:
tgg2 = yo2/(f- xo2) = b/(f(k22+1)+bk2).
Легко показать, что знаменатели этих выражений равны.
Действительно,
f(k22+1)-bk2 = f((k1f-b)/f)2+f+b(k1f-b)/f = k12f+f-bk1,
что и требовалось доказать.
Следовательно, g1 = g2, т.е. треугольник FAN равен треугольнику F/AN, поэтому точка N находится на линзе.
Покажем далее, что g1 = a1+a2.
Действительно,
tg(a1+a2) = (k1-k2)/(1+k1k2) = b/(f(k12+1)-bk2) = tgg1,
что и требовалось доказать.
Поскольку g1 и g2 – внешние углы треугольников С1B1F и С2B2F/, то ![]() ,
, ![]() и, следовательно,
и, следовательно, ![]() и
и ![]() .
.
По теореме синусов для этих треугольников получим:
![]() ,
, ![]() , (13)
, (13)
где ![]() и
и ![]() .
.
Из последних выражений получим
![]() (14)
(14)
Последний знак равенства в (19) появился вследствие того, что точки С1 и С2 оптически сопряженные и, следовательно, связаны формулой Ньютона. Из выражения (13) получим:
![]()
Так как треугольники FO1B1 и F/O2B2 подобные, то
![]() ,
, ![]() ,
,
то есть соотношения (15) выполняются.
Из изложенного следует еще один метод графического определения т. В2 и, следовательно, ![]() и
и ![]() . Соотношение (14) показывает, что точки В1/ и В2/ на оптической оси линзы, расстояние от которых до фокусов F и F/ равны соответственно z1 и z2, оптически сопряжены. Таким образом, если для заданных
. Соотношение (14) показывает, что точки В1/ и В2/ на оптической оси линзы, расстояние от которых до фокусов F и F/ равны соответственно z1 и z2, оптически сопряжены. Таким образом, если для заданных ![]() и
и ![]() найденную точку В1 прямой FN перенести циркулем на оптическую ось (т. В1), а затем построением найти оптически сопряженную ей точку В/2, то после переноса ее циркулем на прямую F/N получим точку В2.
найденную точку В1 прямой FN перенести циркулем на оптическую ось (т. В1), а затем построением найти оптически сопряженную ей точку В/2, то после переноса ее циркулем на прямую F/N получим точку В2.
Формула Ньютона (14), которая связывает x и x' от фокусов линзы до оптически сопряженных точек. А и. А' с учетом упомянутого свойства о перпендикуляре, опущенном из прямого угла на гипотенузу, дает возможность предложить еще один способ графического нахождения изображения линзой некоторой точки А. Для этого от заднего фокуса линзы необходимо отложить отрезок F'A"=FA=-x (по правилу знаков в оптике отрезки, откладываемые от фокуса влево отрицательны, а вправо-положительные). Далее из точки F' отложить отрезок F'd=f', перпендикулярно оптической оси линзы, и тогда, перпендикуляр DA' к прямой A"D, проведенный от точки D при пересечении с оптической осью дает точку A' оптически сопряженную точке A, поскольку для треугольника A"DA' справедливо соотношение f'2 =-xx', полностью соответствующее формуле Ньютона. Указанный метод можно полностью распространить на рассматриваемый случай определения параметров гауссового пучка после линзы. Разница заключается лишь в том, что для гауссовых пучков оптически сопряженными являются отрезки ![]() и
и ![]() соответственно. Поэтому порядок нахождения параметров гауссового пучка, сформированного линзой, будет следующий.
соответственно. Поэтому порядок нахождения параметров гауссового пучка, сформированного линзой, будет следующий.
1) От заднего фокуса вдоль оптической оси линзы откладывают отрезок ![]() , где значение
, где значение ![]() определяет с учетом знака положение перетяжки исходного гауссового пучка относительно переднего фокуса линзы.
определяет с учетом знака положение перетяжки исходного гауссового пучка относительно переднего фокуса линзы.
2) От точки O"1восстанавливают перпендикуляр O"1B"1 равный конфокальному параметру zk исходного гауссового пучка.
3) Из точки F' к получившемуся отрезку B"1F'=-z восстанавливают перпендикуляр F'D длиной f'.
4) Из точки D проводят перпендикуляр к прямой B"1D до пересечения с прямой B"1F' в точке B'1 .
5) Перпендикуляр, опущенный из точки B'1 на оптическую ось линзы, дает точку O'1 , определяющую положение перетяжки пучка после линзы. При этом отрезки F'O'1 и B'1 O'1 дают значение параметров z'p и z'k соответственно.
Для определения радиуса перетяжки трансформированного пучка можно поступить тремя способами. Первый способ предполагает известной конфигурацию огибающей исходного гауссового пучка. В этом случае геометрически определяют радиус пучка rf в передней фокальной плоскости линзы, и затем находят его угловой размер q'=rF/f', представляющий собой расходимость трансформированного пучка.
Тогда ![]() .
.
Второй способ не требует заданной конфигурации исходного пучка. Значение радиуса перетяжки определяют из соотношения

Справедливость этого выражения следует из того, что для исходного и трансформированного гауссового пучков отношение ![]() представляет собой инвариант, поскольку как следует из (2)
представляет собой инвариант, поскольку как следует из (2)
![]()
 (15)
(15)
Третий способ не требует никаких вычислений и знания конфигурации исходного пучка. Его идея состоит в том, что величина r0 в силу (2) и (15) является высотой прямоугольного треугольника, гипотенуза, которого делится ею на части ![]() и
и ![]() , где в исходном пучке отрезок
, где в исходном пучке отрезок![]() в выбранном масштабе. Этот же отрезок следует добавлять вдоль оптической оси к найденному отрезку z'k , после чего следует построить прямоугольный треугольник O'1P'K c гипотенузой O'1K. Высота P'L этого треугольника будет равна радиусу r'0 сечения перетяжки преобразованного гауссового пучка.
в выбранном масштабе. Этот же отрезок следует добавлять вдоль оптической оси к найденному отрезку z'k , после чего следует построить прямоугольный треугольник O'1P'K c гипотенузой O'1K. Высота P'L этого треугольника будет равна радиусу r'0 сечения перетяжки преобразованного гауссового пучка.
Предложенный геометрический метод определения параметров гауссового пучка, преобразованного линзой прост, нагляден и легко может быть реализован с помощью циркуля и линейки. На практике для ускорения построений целесообразно использовать угольник.
Описанный метод легко обобщается на случай произвольного числа линз, преобразующих гауссов пучок.
В тех случаях, когда требуется определить параметры гауссового пучка, изображенного оптической системой с произвольным числом компонентов следует вначале определить кардинальные параметры (положение главных плоскостей и фокусов) всей оптической системы, а затем провести построение как для одиночной линзы. Построением хода нулевого луча 1 определяют положение заднего фокуса F' и задней главной плоскости H'. С помощью второго нулевого луча 2 находят передний фокус F и положение передней главной плоскости H. Перетяжка исходного гауссового пучка, как видно из рисунка, находится на расстоянии – zp от переднего фокуса, а параметр конфокальности пучка равен zk. Этих данных достаточно, чтобы найти положение z'p перетяжки и параметр конфокальности z'k преобразованного пучка. Радиус r'0 определяют одним из способов описанных выше.
ИЗМЕНЕНИЕ ФОРМЫ ГАУССОВОГО ПУЧКА
Рассмотрим теперь вопрос о целенаправленном изменении формы гауссового пучка. Задача формулируется следующим образом: задан гауссовый пучок с известными положением перетяжки и значением параметра конфокальности ![]() . Необходимо определить значение фокусного расстояния линзы f' и ее расстояние от перетяжки XL, чтобы преобразовать заданный гауссов пучок в новый с другим значениям параметра конфокальности
. Необходимо определить значение фокусного расстояния линзы f' и ее расстояние от перетяжки XL, чтобы преобразовать заданный гауссов пучок в новый с другим значениям параметра конфокальности ![]() и новым положением перетяжки, характеризуемым расстоянием d от новой.
и новым положением перетяжки, характеризуемым расстоянием d от новой.
То, что для любых значений ![]() ,
, ![]() и d такая линза существует, следует из предыдущего материала: положение искомой линзы определяется точкой О касания оптической оси окружностью, проходящей через точки В1, В2, L. Отрезок OL является диаметром этой окружности. Если положение линзы будет найдено, то определяются и отрезки ОВ1, ОВ2 и, следовательно, перпендикулярные им отрезки С1В1, С2В2. Точки С1 и С2, в свою очередь, дают возможность геометрическим построением легко определить фокусное расстояние искомой линзы. Как известно, геометрическим местом точек, равноудаленных от заданной прямой и точки, является парабола. Поэтому положение линзы можно определить как абсциссу точки пересечения двух парабол, одна из которых Y1(X) равноудалена от точек В1 и оптической оси, а другая Y2(X) – от точки В2 и оси линзы.
и d такая линза существует, следует из предыдущего материала: положение искомой линзы определяется точкой О касания оптической оси окружностью, проходящей через точки В1, В2, L. Отрезок OL является диаметром этой окружности. Если положение линзы будет найдено, то определяются и отрезки ОВ1, ОВ2 и, следовательно, перпендикулярные им отрезки С1В1, С2В2. Точки С1 и С2, в свою очередь, дают возможность геометрическим построением легко определить фокусное расстояние искомой линзы. Как известно, геометрическим местом точек, равноудаленных от заданной прямой и точки, является парабола. Поэтому положение линзы можно определить как абсциссу точки пересечения двух парабол, одна из которых Y1(X) равноудалена от точек В1 и оптической оси, а другая Y2(X) – от точки В2 и оси линзы.
![]() Выберем начало координат системы XY в точке О1 и запишем уравнения парабол в каноническом виде:
Выберем начало координат системы XY в точке О1 и запишем уравнения парабол в каноническом виде:
(16)
![]() или, после преобразований:
или, после преобразований:
(17)
Поскольку в точке пересечения координаты Y1 = Y2, то, обозначив ![]() и исключив y1 из системы уравнений (21), получим квадратное уравнение относительно x:
и исключив y1 из системы уравнений (21), получим квадратное уравнение относительно x:
![]() (18)
(18)
Дискриминант этого уравнения равен
 |
(19)
(20)
длина отрезка В1В2.
Таким образом, решение уравнения (22) имеет вид
![]() (21)
(21)
Выражение (25) показывает, что существуют два решения поставленной задачи, т.е. существуют две линзы, которые преобразуют исходный гауссовый пучок в пучок с заданными параметрами.
Из (25) видно, что при α = 1 в решении имеется особенность: знаменатель обращается в нуль, но при этом из (24) следует, что l = d, и выражение (22) принимает вид
![]() (23)
(23)
Из (26) видно, что при α = 1 физический смысл имеет только одно решение
![]()
Это означает, что линза должна находиться посередине между исходным и заданным положениями перетяжки.
Определим фокусное расстояние линзы f'.
Запишем :
d+Xp1-Zp2=d+ (1+a)Zp1=2f' (24)
С другой стороны известно, что
![]() (25)
(25)
Из (27) следует
![]() (26)
(26)
Подставим (28) в (27) и после преобразований получим уравнение
![]() (27)
(27)
Дискриминант этого уравнения равен
![]() (28)
(28)
В выражении (31) l – длина отрезка В1В2.
Таким образом, решение уравнения (30) имеет вид
 (29)
(29)
Подставив найденное значение f' в выражение (29), после преобразований получим,
 (30)
(30)
Таким образом, задача аналитически решена. В общем случае она имеет два решения. Величины ![]() , x1 и f' подлежащие определению, находятся из соотношений (33), (25) и (32) соответственно при использовании в них одновременно верхних и нижних чередующихся знаков. Фокусные расстояния линз, соответствующие двум решениям (31) различаются знаками. Действительно:
, x1 и f' подлежащие определению, находятся из соотношений (33), (25) и (32) соответственно при использовании в них одновременно верхних и нижних чередующихся знаков. Фокусные расстояния линз, соответствующие двум решениям (31) различаются знаками. Действительно:
![]()
Подводя итоги изложенному, можно предложить следующий графоаналитический метод решения задачи преобразования гауссового пучка:
1. Для заданных значений ![]() ,
, ![]() и d откладывают от оси отрезки O1B1 =
и d откладывают от оси отрезки O1B1 = ![]() и O2B2 =
и O2B2 = ![]() определяют значение
определяют значение ![]() и рассчитывают одно из значений X1 (для положительной или отрицательной линзы). Длина l определяется графически (l=В1В2 с учетом масштаба) или аналитически – по формуле (24).
и рассчитывают одно из значений X1 (для положительной или отрицательной линзы). Длина l определяется графически (l=В1В2 с учетом масштаба) или аналитически – по формуле (24).
2. Откладывают от т.О1 отрезок X1 вдоль оптической оси и получают т.О – центр линзы.
3. Из точки О откладывают отрезки ОВ1 и ОВ2, а затем – прямые LC1 и LC2, перпендикулярные этим отрезкам.
4. Положение фокусов F и F′ линзы, длины отрезков ![]() и
и ![]() , характеризующие положения перетяжек относительно фокусов, определяются графическими построениями для линзы при условии оптической сопряженности точек С1и С2.
, характеризующие положения перетяжек относительно фокусов, определяются графическими построениями для линзы при условии оптической сопряженности точек С1и С2.
5. Аналогичные операции (2 - 4) выполняются и для другого варианта X1.
Изложенный алгоритм является графоаналитическим. Он предполагает проведение некоторых расчетов и последующих геометрических построений.
Можно предложить также способ геометрического определения параметров линзы, осуществляющей заданную трансформацию лазерного пучка. Сущность этого способа заключается в том, что отрезок MN1, определяющий искомое положение линзы по теореме о касательной и секущей, выражается следующим образом:
![]()
Здесь точка M есть точка пересечения прямой B1B2 с оптической осью. Если из точки B2 провести перпендикуляр к прямой B1B2 и на отрезке B1M как на диаметре построить окружность, то она пересечет этот перпендикуляр в точке E, а угол MEB1будет прямым. Тогда по второй теореме о перпендикуляре, опущенном из прямого угла на гипотенузу, получим:
![]()
то есть отрезок ME равен искомому отрезку MN. Таким образом, если из точки M циркулем перенести отрезок ME на ось, мы получим точку N – положение линзы. Если затем провести из точки N прямые к точкам B1 и B2 и затем восстановить перпендикуляры к ним в этих точках, то точки пересечения C1 и C2 этих перпендикуляров с оптической осью будут оптически сопряженными точками. После этого графическое определение положения фокусов линзы не представляет никаких затруднений.
ЗАКЛЮЧЕНИЕ
На основе материала, изложенного в работе, можно сделать следующие выводы:
1. Несмотря на то, что понятие геометрической и гауссовой оптики несовместимы, основные положения теории дифракции применительно к гауссовым пучкам обуславливают возможность использования наглядных и простых геометрических методов, как для описания гауссовых пучков, так и для преобразования их оптическими элементами.
2. Показано, что геометрические методы могут быть использованы не только для анализа преобразования гауссового пучка оптическими элементами, но и для синтеза оптической системы, преобразующей исходный лазерный пучок в гауссовый с заданными параметрами.
3. Поскольку наглядность является важнейшим элементом образовательного процесса, мы убеждены, что изложенные в работе методы могут широко использоваться в преподавательской работе как образовательный инструмент.
Список литературы
1. Пахомов И.И., Цибуля А.Б. Расчет оптических систем лазерных приборов. – М.: Радио и связь, 1986. – 140 с.
2. Джерард А., Берч Дж.М. Введение в матричную оптику: Пер. с англ. / Под ред. В.В.Коробкина. – М.: Мир, 1978. – 340 с.
3. Заказнов Н.П., Кирюшин С.И., Кузичев В.И. Теория оптических систем. – М.: Машиностроение, 1992. – 447 с.
4. Пахомов И.И. Расчет преобразования лазерного пучка в оптических системах. – М.: МГТУ им. Н.Э.Баумана, 1998. – 54 с.
Публикации с ключевыми словами: дифракция, эрмито-гаусовый пучек, преобразование линзой, оптический элемент
Публикации со словами: дифракция, эрмито-гаусовый пучек, преобразование линзой, оптический элемент
Смотри также:
- Исследование задач трехмерной газодинамики на примере задачи о дифракции ударной волны на трехмерном уступе
- Результаты решения задач дифракции на телах большого электрического размера с использованием программы FEKO
- Экспериментальные исследования процесса плазмохимического травления стекла при изготовлении дифракционных и голограммных оптических элементов
Тематические рубрики:
| Авторы |
| Пресс-релизы |
| Библиотека |
| Конференции |
| Выставки |
| О проекте |
| Телефон: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) |
|
||||
| © 2003-2024 «Наука и образование» Перепечатка материалов журнала без согласования с редакцией запрещена Тел.: +7 (915) 336-07-65 (строго: среда; пятница c 11-00 до 17-00) | |||||



